- 著者
- 畝山 多加志
- 出版者
- 一般社団法人 日本物理学会
- 雑誌
- 日本物理学会誌 (ISSN:00290181)
- 巻号頁・発行日
- vol.76, no.10, pp.663-668, 2021-10-05 (Released:2021-10-05)
- 参考文献数
- 22
物性の研究ではマクロスケールの(巨視的な)物性について測定や解析が行われることが多い.マクロスケールの物質の示す複雑な緩和や応答も元をたどれば究極的にはミクロスケールの(微視的な)分子や原子の構造に還元できると期待される.これは物理(特に統計力学)の考え方としては標準的なものであろう.ソフトマターのように構成要素が複雑な場合には,ミクロスケールとマクロスケールの中間であるメソスケールにおいて特徴的な構造や運動をもつことがある.この場合もやはりメソスケールの挙動は究極的にはミクロスケールに還元できると考えられる.原理的には分子や原子の初期状態の位置と運動量がわかれば系の時間発展は一意に決まるのだから,メソスケールだろうとマクロスケールだろうとミクロスケールの情報からすべて計算が可能なように思える.もちろん,初期状態を完全に知ることはできないし,カオス的な振る舞いもあるため状況はそこまで単純ではない.メソスケールの運動や緩和,あるいはメソスケールの情報を強く反映するマクロスケールの物性を理解するには,メソスケールの運動を直接的に記述し解析することが望ましい.これはミクロスケールの情報のうち興味ある一部の情報(着目する粒子の位置や運動量)のみを取り出す粗視化とよばれる手法を用いて実現できる.粗視化によって消える自由度の効果は系統的に取り込め,未知の初期状態の影響はランダムな揺動力という形で運動方程式中に現れる.このランダムな揺動力がBrown運動の起源となり,粒子の運動の軌跡は不規則な形状を呈することになる.さらに,粒子の感じるポテンシャルや時間遅れの効果等を取り込むことで,メソスケールの運動の一般的記述が可能になるとされている.ところが,このような手法で十分に一般的なメソスケールの運動を記述可能かというと,実はそうではない.既存の手法で記述不可能な対象が少なからず存在するのである.例えば,高分子の運動は分子同士が互いにすり抜けられないという動的な拘束のために単純な形では記述できない.近年,そのようなある種の特殊なBrown運動の記述について,新しい視点からのモデル化や理解が進展しつつある.メソスケールの系を記述する際に通常着目する自由度である位置や運動量に加えて,拡散係数やポテンシャルといった量も自由度として考慮するというものである.従来の方法では,拡散係数やポテンシャルは環境の効果を平均化したものであり,平均値からのずれがランダムな揺動力として取り扱われていた.これに対して,新しい方法では,拡散係数やポテンシャル自体が時々刻々と変化する環境の影響を受けてランダムに変化する量であるとする.一見,ランダムに変化する部分が変わっただけでさほどの影響がないように思えるかもしれないが,ゆらぐ拡散係数やポテンシャルを使うことで従来の方法とは定性的に異なる運動を記述することができる.ゆらぐ拡散係数やポテンシャルを用いた新しい方法は新しい運動方程式のクラスを形成しているものと考えられる.新しい方法はソフトマターをはじめとしたさまざまな系に適用できるものと期待される.例えば,高分子の動的な拘束を表現するために各論的・現象論的にさまざまな運動モデルが提案されているが,これらをゆらぐ拡散係数やポテンシャルを使った枠組みで統一的に解釈し直すことができる.また,過冷却液体中の分子の示す一時的にトラップされるような運動も,新しい方法を用いることで単純な形で記述することができる.
- 著者
- 畝山 多加志
- 出版者
- 公益社団法人 高分子学会
- 雑誌
- 高分子論文集 (ISSN:03862186)
- 巻号頁・発行日
- pp.2018-0035, (Released:2018-10-11)
- 参考文献数
- 18
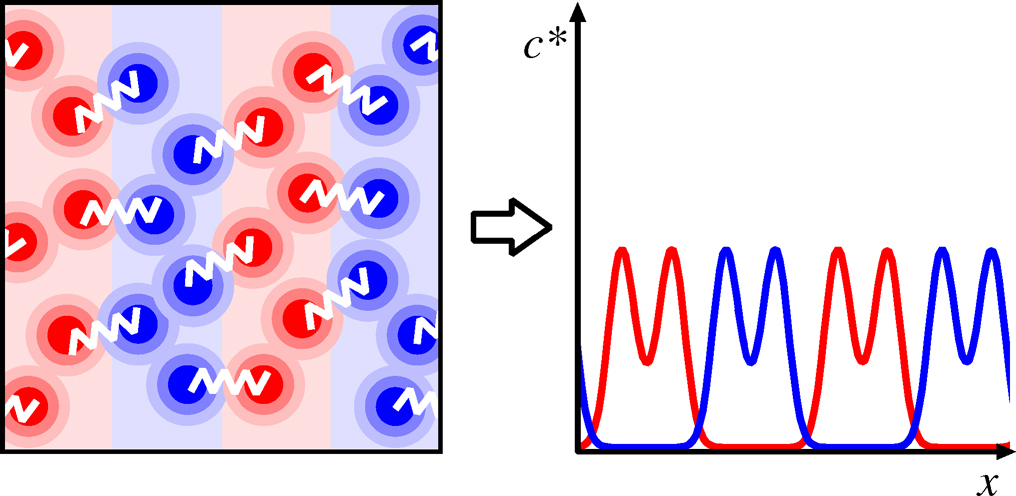
対称ジブロックコポリマーのミクロ相分離構造を取り扱うための粗視化モデルとして,ソフトダンベルモデルに基づく自己無撞着場(SCF)理論を提案する.二つの粗視化粒子を連結することでジブロックコポリマーを表現するソフトダンベルモデルに対して標準的なSCFモデルの導出手法を適用することで濃度場と外場に対する自己無撞着な連立方程式を導出する.得られたSCFモデルを用いて一次元系でシミュレーションを行うことで,ミクロ相分離構造を再現できることを示す.また,得られたSCFモデルの性質について考察を行う.