- 著者
- 熊野 裕太
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.1, no.2, pp.[1], 2012-08
8 0 0 0 OA Frohlich理論について
- 著者
- 中嶋 貞雄
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1953, no.65, pp.116-130, 1953 (Released:2009-11-26)
- 参考文献数
- 10
7 0 0 0 OA ひとつの電気伝導計算法
- 著者
- 中野 藤生
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1955, no.84, pp.25-34, 1955 (Released:2010-12-10)
- 参考文献数
- 2
7 0 0 0 OA <講義ノート>"人工知能"のための統計力学
- 著者
- 樺島 祥介
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.3, no.1, pp.[1], 2014-02
6 0 0 0 OA 超電導電子集団の量子流体力学
- 著者
- 御子柴 宣夫
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1954, no.76, pp.13-21, 1954 (Released:2009-11-26)
- 参考文献数
- 10
4 0 0 0 OA 水素分子の分極率について
- 著者
- 石黒 英一 荒井 正 小谷 正雄 水島 正喬
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1951, no.42, pp.1-16, 1951 (Released:2009-11-26)
- 参考文献数
- 16
- 著者
- 大久保 絢夏 小沼 瞳 横川 真衣 遠藤 美貴 栗橋 愛 沢畠 博之 北畑 裕之 Tomio Petrosky
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.2, no.1, pp.[1], 2013-02
- 著者
- 松井 卓
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.4, no.4, 2015-11
第60回物性若手夏の学校の講義のテキスト
4 0 0 0 OA <講義ノート>水の計算物理学とデータマイニング
- 著者
- 松本 正和
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.3, no.3, pp.1-17, 2014-08
4 0 0 0 OA <講義ノート>量子力学の基礎に関する最近の話題
- 著者
- 筒井 泉
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.3, no.1, pp.[1], 2014-02
3 0 0 0 IR <講義ノート>増殖過程の統計物理的構造(第61回物性若手夏の学校 集中ゼミ)
- 著者
- 小林 徹也
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.6, no.4, 2017-11
第61回物性若手夏の学校 集中ゼミ一般の物理系と異なり、細胞や個体などの生物集団は、自己の状態を変異させ、また自身の複製を生成することで増殖をすることができる。この変異と増殖のダイナミクスは生命進化を司る基本過程であり、その理解は非生物系と生物系の共通構造および本質的な差異を解明するためにも必須である。また、生物系は積極的に環境の情報を内部に取り込みそれを処理することにより、集団としての適応度(増殖率)を制御することができる。適応度と情報の関係を理解することは、我々の脳のような高度な情報処理機構が進化の過程でどのように選択されてきたのかを明らかにするためにも重要である。この問題に関し、本発表では増殖過程の有する数理構造に着目する。具体的には、増殖ダイナミクスの経路積分表現とそれに伴う遡及的表現を導入することにより、増殖過程に内在する統計物理的構造を明らかにする。この構造を用いることにより、確率熱力学と同様に、増殖集団の適応度などのマクロな諸量に成り立つゆらぎ関係を示す。また、この表現を活用することで、適応度と情報に成り立つ交換関係を、統一的に明らかにする。これらの生物学的な意義を議論するとともに、進化の問題への他の物理的アプローチの可能性についても言及をする。
2 0 0 0 OA <修士論文>つながりと初期条件が及ぼす流行現象への影響
- 著者
- 岩井 淳哉
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.2, no.3, pp.[1], 2013-08
2 0 0 0 OA 非可逆過程の熱力学と量子統計力学
- 著者
- 中嶋 貞雄
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1956, no.102, pp.24-31, 1956 (Released:2009-11-26)
- 参考文献数
- 6
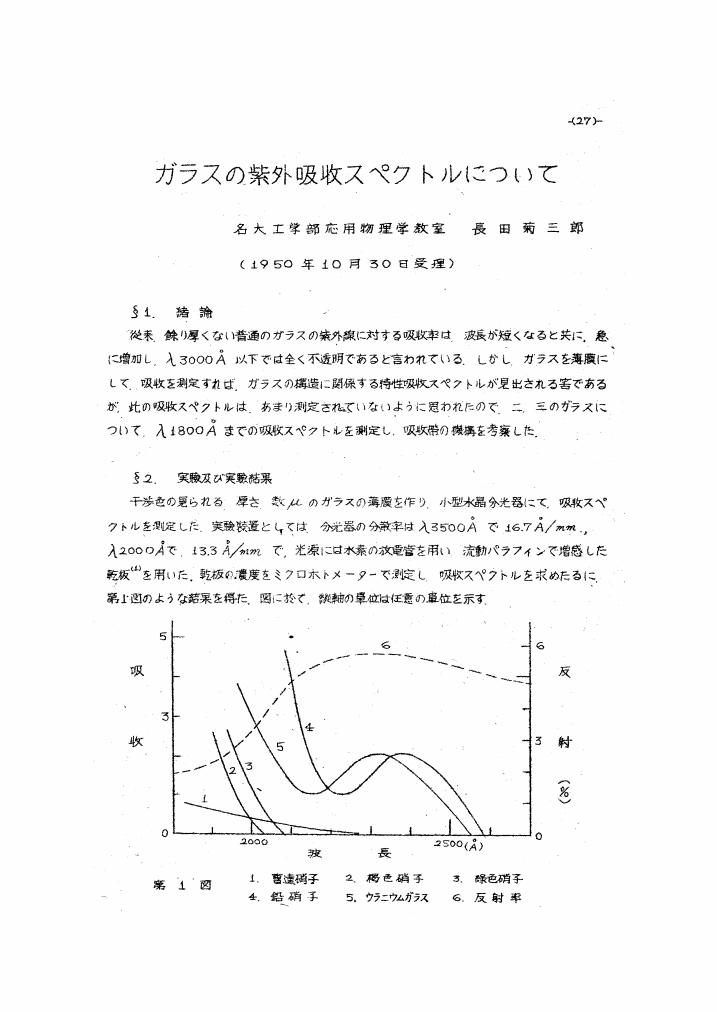
1 0 0 0 OA ガラスの紫外吸収スペクトルについて
- 著者
- 長田 菊三郎
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1950, no.32, pp.27-29, 1950 (Released:2009-11-26)
- 参考文献数
- 7
1 0 0 0 OA 液体ヘリウムの格子模型
- 著者
- 松原 武生
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1956, no.99, pp.52-61, 1956 (Released:2009-11-26)
- 参考文献数
- 3
1 0 0 0 OA <講義ノート>情報処理の熱力学 (第59回物性若手夏の学校 : 集中ゼミ)
- 著者
- 沙川 貴大
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性研究・電子版
- 巻号頁・発行日
- vol.4, no.1, pp.1-16, 2015-02
情報理論と熱力学を融合した理論, 情報熱力学について入門的な解説を行う. とくに, 測定やフィードバックなどの情報処理過程への, 熱力学第二法則や非平衡関係式の一般化について議論する. また, 情報熱力学の一つの帰結として, いわゆるマクスウェルのデーモンのパラドックスがどう解決されるかも議論する
1 0 0 0 OA 量子統計力学における密度行列の展開
- 著者
- 久保 亮五
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1951, no.38, pp.24-41, 1951 (Released:2009-11-26)
A general theorem is proved on the density matrix of quantum statistics. Let the de sity matrix be ρ {M} =exp [-βΣMl=1Hl], in which the operators Hl's are not always commutable. ρ {M} can be expanded in series of the formρ {M} =ΣMΣmi=0 n≥0 Σ {ml} M--- {mn} Mρ* {mM1} ---ρ* {mn} ρ {M-m1----mn} where. the sets {m1}, --- {mn} are groups of operators chosen from the set {M} and operators belonging to different groups are commutable. The summation is to be taken over all the possible choice of the sets {m1} --- {mn}.ρ {k} is defined byρ {k} = [Π {k} exp (-βHj)] s where suffix s means the symmetrization by changing the order of the products. And ρ* {m} is defined byρ* {m} =Σ {k}l (-) m-k ρ {k} ρ {m-k} which is proved to be 0 (βm+1). the series expansion here proved is very useful in quantum statistics.
1 0 0 0 OA 三中心エネルギー積分に関する研究I
- 著者
- 永原 茂
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1953, no.69, pp.205-216, 1953 (Released:2010-02-26)
- 参考文献数
- 4
The formula for the one-electron three-center molecular integral may be written Kc;AB=∫xa(1) 1/rc1xb(1) dτ1≡ (xa|1/rc1|xb) Using the slater-type as the AO's and expressing in terms of the fixed elliptical coordinates (ξc, ηc and φc) of the center C and the coordinates (ξ, η, φ) of the electron, in the conventional manner by the Neumann expansion, we obtain as follows. Kc;AB=C∑Dτνw°njGντ (j : β) Rντ (n, α : ξc) Pντ (ηc) cosνφc sinνφc where Gντ (j : β) =∫1-1ηje-ρηPντ (η) (1-η2) ν/2dη Rντ (n, α : ξc) =∫∞1Qντ (ξ+) Pντ (ξ-) ξne-αξ (ξ2-1)ν/2dξ (defined as Mτ (ξc, n, α) by H.Eyring) R0τ (n, α : 1) =fτ (n, α) (values tabulated by Prof.Kotani) C=a constant
1 0 0 0 OA 統計力學における一つの解析的方法
- 著者
- 久保 亮五
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1943, no.1, pp.1-13, 1943-08-05 (Released:2009-11-26)
1 0 0 0 OA 量子力学に対する位相空間分布の方式について
- 著者
- 高林 武彦
- 出版者
- 物性研究・電子版 編集委員会
- 雑誌
- 物性論研究 (ISSN:18837808)
- 巻号頁・発行日
- vol.1953, no.66, pp.48-72, 1953 (Released:2009-11-26)
- 参考文献数
- 7
The formulation of quantum mechanics in terms of the ensemble in phase space is investigated in some points. The subsidiary conditions for the phase space ensemble to represent a pure state are clarified, and the equivalence between this formulation and the alternative one in terms of quantum potential is verified.