7 0 0 0 OA 竹の節・組織構造が織り成す円筒体としての合理的な構造特性の理論的解明
- 著者
- 佐藤 太裕 谷垣 俊行 佐藤 諭佳 島 弘幸 井上 昭夫
- 出版者
- 公益社団法人 土木学会
- 雑誌
- 土木学会論文集A2(応用力学) (ISSN:21854661)
- 巻号頁・発行日
- vol.72, no.2, pp.I_25-I_34, 2016 (Released:2017-01-29)
- 参考文献数
- 26
- 被引用文献数
- 1 5
自然界に生息するタケは中空円筒であり,かつ節と組織構造を有する植物である.これは適者生存の厳しい環境下でできるだけ強く,高く生育するためにタケ自身が進化の過程で獲得してきた形態であり,力学的に極めて高い合理性を有すると考えられる.本研究は,タケの生態を構造力学的に紐解き,節配置の高さ方向分布と維管束の横断面内分布の不均一性が織り成す力学的優位性を実証するものである.この研究により,曲げを受けるタケの節配置による断面偏平抑制効果を剛性に関する異方性を考慮した無次元パラメータにより記述し,タケが外力により生じる曲げモーメント分布に合わせて断面偏平を効率的に抑制していること,また横断面内維管束分布は曲げ剛性を高めるように効果的に配置されていることが初めて理論的に示された.
4 0 0 0 OA トガリネズミ (Sorex) の歯の着色と組織構造
- 著者
- 小沢 幸重 三島 弘幸 寒河江 登志朗 奥田 綾子
- 出版者
- Japanese Association for Oral Biology
- 雑誌
- 歯科基礎医学会雑誌 (ISSN:03850137)
- 巻号頁・発行日
- vol.30, no.1, pp.31-40, 1988-02-20 (Released:2010-06-11)
- 参考文献数
- 32
トガリネズミ (食虫類) の歯の構造と着色について検討した。着色は, 各歯の接触面のエナメル質, 即ち上顎では口蓋側面, 下顎は唇側および頬側面にある。着色は, 齧歯類の切歯と同様にエナメル質への鉄の沈着によるものであるが, 歯列弓の歯のすべてに認められる。着色エナメル質は最大でエナメル質全層の表面側2/3~3/4層におよびその下層は無着色エナメル質である。鉄の含有量はSEMの非分散型定量分析では約8% (重量比) である。トガリネズミのエナメル質は, 細管エナメル質と無細管エナメル質無小柱エナメル質と有小柱エナメル質の4組織を持っている。エナメル細管はほぼエナメル質の全領域に認められるが, 着色エナメル質には非常に少なくほぼ無細管の状態である。エナメル小柱は, 比較的単純なコースをエナメル象牙境からエナメル質表面まで走向するが, 非常に薄い咬頭間領域のエナメル質では認められない。シュレーゲルの条紋は観察されないが, 無着色エナメル質のエナメル小柱は小柱問エナメル質を狭むようにして平行に配列する。エナメル小柱の直径は, 約3 μmである。エナメル細管は屈曲走行し, 象牙細管に連続する。以上の構造のいくつかは, 初期哺乳類の構造と一致するものであり, 下等な哺乳類と高等な哺乳類の移行的構造であろう。象牙質は管周象牙質が発達し, セメント質は非常に薄い。
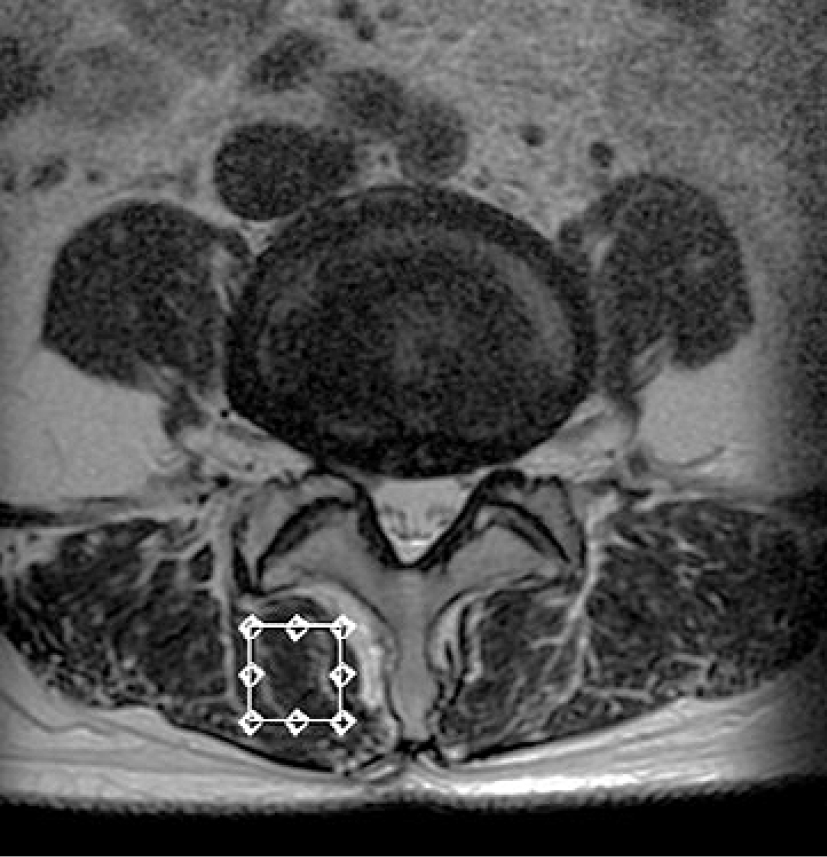
4 0 0 0 OA 慢性腰痛患者における腰痛の改善に伴う多裂筋の筋細胞内脂肪の変化
- 著者
- 高島 弘幸 黄金 勲矢 竹林 庸雄 押切 勉 森田 智慶 吉本 三徳 寺島 嘉紀 山下 敏彦
- 出版者
- 一般社団法人 日本脊椎脊髄病学会
- 雑誌
- Journal of Spine Research (ISSN:18847137)
- 巻号頁・発行日
- vol.11, no.6, pp.897-901, 2020-06-20 (Released:2020-06-20)
- 参考文献数
- 15
慢性腰痛患者では,多裂筋の筋細胞内脂肪(intramyocellular lipids:IMCL)が上昇していることが報告されている.本研究では,慢性腰痛患者における多裂筋のIMCLが腰痛の経過とともにどのように変化するかを縦断的に解析した.腰痛VASの改善率とIMCLの変化率の間には,正の相関(r = 0.818,p < 0.001)が認められ,腰痛の改善とともにIMCLが低下する傾向であった.多裂筋のIMCLは,慢性腰痛と深い関連があることが示唆された.
2 0 0 0 OA 光学メディアによる光干渉Duo-Rainbowの教材提案
- 著者
- 吉川 佳佑 島 弘幸
- 出版者
- 一般社団法人 日本科学教育学会
- 雑誌
- 日本科学教育学会研究会研究報告 (ISSN:18824684)
- 巻号頁・発行日
- vol.32, no.6, pp.33-36, 2018-03-25 (Released:2018-07-01)
- 参考文献数
- 2
虹をテーマとした「光の回折・干渉」の実験は、目にした生徒の印象に残りやすく、光の波動性を学ぶのに適した実験の一つである。本稿では光ディスク(CD やDVD 等)を用いて、二重同心円の虹模様を、教室の壁いっぱいに作り出す手法を紹介する。本手法で二重の虹の円を実演した後、その仕組みを生徒に考えさせることで、回折・干渉に関する生徒の理解を促すことができる。さらに手軽で安全な道具のみを用いることから、生徒自身が実験条件を自由に工夫して、虹の変化を楽しむことができる。
2 0 0 0 対人運動技能の制御・学習則の解明
本研究では,スポーツにおける対人運動技能の制御・学習則を解明する.対人運動技能とは,眼前の他者と連携や駆け引きを行う技能と,連携や駆け引きを通して互いに成長し続ける技能の両方を指す.これは様々なスポーツに共通の重要な技能であると考えられるが,従来は個の運動技能のみが扱われており,対人運動技能の制御・学習則は未知である.そこで本研究では,二者が連携や駆け引き,二者が連携して他の二者と駆け引きする対人運動技能の制御・学習過程の調査・行動実験からそこに潜む規則性を見つけ,数理モデルを構築して制御・学習の本質を理解し,ロボットに実装してその妥当性を検証する.
- 著者
- 島 弘幸 中山 恒義
- 出版者
- 一般社団法人 日本物理学会
- 雑誌
- 日本物理学会講演概要集
- 巻号頁・発行日
- vol.59, 2004
1 0 0 0 OA メラトニンの新規作用:骨に対する作用とその誘導体を用いた骨疾患治療薬の開発
1 0 0 0 光学メディアによる光干渉Duo-Rainbowの教材提案
- 著者
- 吉川 佳佑 島 弘幸
- 出版者
- 一般社団法人 日本科学教育学会
- 雑誌
- 日本科学教育学会研究会研究報告
- 巻号頁・発行日
- vol.32, no.6, pp.33-36, 2018
<p>虹をテーマとした「光の回折・干渉」の実験は、目にした生徒の印象に残りやすく、光の波動性を学ぶのに適した実験の一つである。本稿では光ディスク(CD やDVD 等)を用いて、二重同心円の虹模様を、教室の壁いっぱいに作り出す手法を紹介する。本手法で二重の虹の円を実演した後、その仕組みを生徒に考えさせることで、回折・干渉に関する生徒の理解を促すことができる。さらに手軽で安全な道具のみを用いることから、生徒自身が実験条件を自由に工夫して、虹の変化を楽しむことができる。</p>
1 0 0 0 OA 悪路で自然発生する波状起伏の機構解明とそれに基づく道路管理技術の新構築
1 0 0 0 OA ラーメンスープの旨味成分に関する研究(I) : イノシン酸の追求
- 著者
- 平岡 英一 野村 明 島崎 琴子 三島 弘幸
- 出版者
- 学校法人高知学園 高知学園短期大学
- 雑誌
- 高知学園短期大学紀要 (ISSN:03894088)
- 巻号頁・発行日
- vol.38, pp.57-67, 2008 (Released:2021-05-07)
This study was carried out to detect umami substances (IMP: inosine monophosphate, MSG: monosodium glutamine, GMP: guanosine monophosphate) in ramen noodle soup-broth sold in restaurants and retail supermarkets in Kochi Prefecture, Japan. In particular, our study examined the connection between IMP and prefered salt levels found in blind taste test conducted by Kochi Gakuen College nutrition students. According to the analysis from our samples, the average level of IMP found in restaurant ramen soup-broth was 0.42μM/ml IMP and 0.82μM/ml in commercially sold soup-broth. However, students chose a level of 5.3μM/ml IMP as the most delicious. In both restaurant and commercial soup-broth, IMP levels varied greatly; however, the level of salt present varied slightly, the average restaurant soup-broth was 1.57% and 1.6% in commercial soup-broth. The students, however, chose a salt level of 1.1% as the most desirable from a taste standpoint. In this case, there was little difference between the students' preferences and what is commonly available in restaurants and supermarkets. Finally, based on the findings, we tried to make the most delicious ramen soup-broth by adjusting the levels of salt and IMP in supermarket soup-broth to 1% and 1.57μM/ml, respectively.
1 0 0 0 環境の幾何学条件に応じた役割切替え能力の発達
小学校2, 4, 6年生を対象とした実験を完了し,以下の結果を得た(現状も分析を続行している).1) 三者跳躍課題の遂行に伴うミスの回数を学年間で比較した結果,第2学年以上になるとミスの回数が多くなる傾向が見られた.2年生においては一方向のみあるいは定型的に跳躍方向を切り替える組(例えば,左右1回ずつ交互に,あるいは2回ずつ交互になど)が7割がたを占め,第4学年以上になると不規則に跳躍方向を切り返す組が7割がたを占めていた.また第6学年では成人と同じく,反時計回り方向へ跳躍するケースが顕著に多くなった(平均で成功回数の7割).2)先導跳躍者に対する他二者の遅れに関して学年間に有意差はなかったが,全ての学年における遅れ時間が,成人より有意に大きかった.また先導・追従性に差がない等質群においては,成人と同じく,正方形条件における遅れが正三角形条件における遅れより大きい傾向があった.また先導性に差がある異質群においては,成人とは逆に,正方形条件において先導児童が早期に跳躍することを示す二者先導(一者追従)型の協応パタンを示す傾向が強かった.3)等質群では,三者の配置が対称な正三角形条件において三者それぞれが他を先導する確率が等しく(約33%),正方形条件では跳躍方向に空き地を持つ一者が先導する確率が抜きん出て高く,他の二者が先導することはほとんどなかった.これら協応パタンは成人のパタンと同じ性質であり,それぞれの地形における跳躍者の配置の対称性から群論に基づいて予測したパタンと一致する.一方で異質群においては先導児童が場の制約に反して先導する傾向が高かった.そこで現れるパタンの時空間対称性は地形から予測される対称性より低い.現在,跳躍者の個性が地形の幾何学対称性から予測される協応パタンの対称性が,そこに配置される跳躍者の個性によって崩れることを説明する数理モデルを検討している.
1 0 0 0 OA サッカーの攻防に潜む連成振動
- 著者
- 山本 裕二 横山 慶子 木島 章文 島 弘幸 YAMAMOTO Yuji YOKOYAMA Keiko KIJIMA Akifumi SHIMA Hiroyuki
- 出版者
- 名古屋大学総合保健体育科学センター
- 雑誌
- 総合保健体育科学 (ISSN:02895412)
- 巻号頁・発行日
- vol.40, no.1, pp.1-14, 2017-06-30
This study considered the movements of the defense lines and the ball during a football game as a three-coupled oscillation. Each defense line of two opposing teams oscillated with in-phase synchronization, and the length between each defense line and the ball oscillated with anti-phase synchronization. We introduced a three-coupled oscillation model to understand these synchronizations. First, we considered the case in which three masses, m, and four spring constants, k, were equal in a three-coupled oscillation. We calculated the eigenvectors and eigenvalues based on the equation of motion, and we obtained three modes of oscillation as three angular frequencies in the equation. We obtained key parameters when we defined the initial state of the system, which allowed us to solve the equation of motion for three-coupled oscillation. Next, we considered cases in which three masses and four spring constants differed. To confirm the validity of the three-coupled oscillation model, we calculated the distribution of the relative phase between two outer masses, m1 and m3, as defense lines and the length between two outer masses and the middle mass, m2, as each defense line and the ball. The three-coupled oscillations showed similar distributions of the relative phase. However, the periodogram showed distinct periodicity. Thus, a more sophisticated model is needed to understand the behavior of the defense lines and the ball during football games.
1 0 0 0 OA メラトニン投与による象牙質の組成や組織構造の変化に関する分析学的及び組織学的研究
- 著者
- 三島 弘幸 門田 理佳 尾﨑 真帆 服部 淳彦 鈴木 信雄 筧 光男 松本 敬 池亀 美華 見明 康雄
- 出版者
- 日本再生歯科医学会
- 雑誌
- 日本再生歯科医学会誌 (ISSN:13489615)
- 巻号頁・発行日
- vol.12, no.1, pp.11-22, 2014 (Released:2016-05-11)
- 参考文献数
- 20
- 被引用文献数
- 1
本研究はメラトニンが象牙質の組成や組織構造に及ぼす影響を分析学的及び組織学的に解析することを目的とした.本研究は出生後5日,6日,7日令のSDラットを用いた.メラトニン投与群では象牙前質に石灰化球が多く見られ,投与濃度上昇につれ象牙前質中の石灰化球数は増加し,大きさも大きくなった.ALP染色は対照群と比べて高濃度群により強い青紫色のALP発現が見られ,メラトニン投与濃度が上昇するにしたがって,象牙芽細胞のALP発現が強くなった.SEM-EDS分析,EPMA分析では,昼間,夜間試料共に投与群でCa及びPが多く含有していた.顕微レーザーラマン分光分析は,PO43-ピークが高濃度群でピークが高く,半価幅も狭まり,メラトニン投与によって,PO43-の分子配向性,アパタイト結晶性が良好となった事が判明した.メラトニンは象牙質の組織形成を促進し,石灰化を亢進し,象牙質の石灰化に影響を及ぼすと考察される.
- 著者
- 三島 弘幸 間島 信男
- 出版者
- 埼玉県立自然の博物館
- 雑誌
- 埼玉県立自然史博物館研究報告 (ISSN:02885611)
- 巻号頁・発行日
- no.17, pp.5-12, 1999-12-25
1 0 0 0 これで決まり MR撮像パラメータ設定
- 著者
- 信田 修壱 原田 邦明 川崎 伸一 森山 兼司 安田 浩司 上野 昌之 高島 弘幸
- 出版者
- 公益社団法人 日本放射線技術学会
- 雑誌
- 日本放射線技術学会雑誌 (ISSN:03694305)
- 巻号頁・発行日
- vol.63, no.7, pp.796-805, 2007-07-20 (Released:2007-10-04)
(抄録はありません)
- 著者
- 松尾 陽 沢地 孝男 羽田野 健 福島 弘幸
- 出版者
- 一般社団法人日本建築学会
- 雑誌
- 学術講演梗概集. D, 環境工学 (ISSN:09150145)
- 巻号頁・発行日
- vol.1985, pp.749-750, 1985-09-10